Una explicación matemática a por qué las listas de consejos no sirven para nada

Se acercan las comidas propias de estas fechas en las que celebramos el triunfo del día sobre la noche a partir del solsticio de invierno e, irremediablemente, la mayoría tendremos que escuchar con paciencia a algún familiar, posiblemente un cuñado, que nos regala sus mejores consejos sobre qué hacer con nuestras vidas. Como dice mi madre, son dos días al año, qué trabajo te cuesta escucharlo y ser amable. Pero esta maña 'cuñadil' ha traspasado fronteras y es difícil terminar el día sin encontrar en la red alguna entrada del tipo “10 consejos para...”.

Voy a dar hoy un consejo: No deis consejos.

Y no solo porque a los demás les puede llegar a cansar sino porque si seguimos todos los mismos consejos y convergemos todos al mismo perfil, ya sea como humano o como usuario de Twitter, Facebook, Instragram, Flickr... no habrá evolución, no mejoraremos. Puede que todos lleguemos a ser un poco mejor, pero no llegaremos a las cotas más altas porque no existirá el elemento diferenciador que produzca la mutación necesaria para mejorar la especie.

Huy, que serio y profundo me ha quedado. Voy a explicarlo con matemáticas que me resulta más fácil. Al menos, voy a intentarlo.

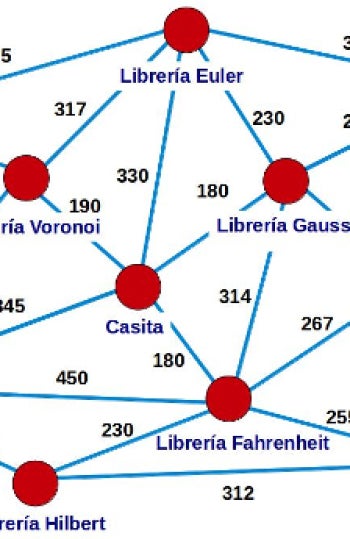
Existen problemas de optimización (encontrar el mejor valor para una determinada función objetivo: costes, beneficios, tiempo...) que no es posible resolver usando los métodos clásicos, ni siquiera aprovechando la potencia de un ordenador. Uno de los más típicos de este tipo de problemas se conoce como el problema del viajante (TSP, de sus siglas en inglés). El planteamiento del TSP es muy simple: dado un conjunto de ciudades conectadas por carreteras, se trata de diseñar la ruta más corta que saliendo desde un determinado punto, recorra todas las ciudades y vuelva a dicho punto de partida. Nuestra amiga Mati lo contó aquí. Por ejemplo, en la figura siguiente, se trataría de diseñar una ruta que, saliendo desde el punto marcado como casita, pasara por todas las librerías del plano y volviera al principio.

En un primer acercamiento a este problema, alguien podría pensar, y tiene razón, que para resolverlo basta con probar con todas las rutas posibles, intercambiando el orden de las ciudades visitadas, calcular la longitud de cada una de esas posibles rutas y quedarse con la más corta. Bien. Salvo por el pequeño detalle de que esta solución solo es posible de calcular para un número muy pequeño de ciudades. Para que nos hagamos una idea, si tenemos 100 ciudades, el número de rutas posibles es 100! (factorial de 100, no es que esté gritando) y 100!, créanme, es un número una 'jartá' de grande. Es mucho más grande que el número de partículas elementales en el universo observable. Por lo tanto, este primer intento de solución no es válido ni con la potencia de cálculo de los ordenadores.

¿Qué hacemos cuando no podemos encontrar la solución óptima (la mejor) ni siquiera con ordenadores? Pues tratar de buscar la más buena posible, por aquello de que a falta de pan... Para ello, lo que se puede usar, por ejemplo, son los llamados algoritmos genéticos: algoritmos que tratan de simular el proceso darwinista mediante el cual la naturaleza consigue especies que se adapten a su medio.

Voy a intentar explicarlo con un ejemplo del problema TSP.

Supongamos que tenemos 6 ciudades a las que denominamos A, B, C, D, E y F. Tratamos de encontrar la permutación óptima de dichas letras que nos de la distancia mínima (saliendo de A y volviendo a A). Los elementos que componen nuestro algoritmo genético son los siguientes:

--Una población inicial: Esta población inicial tendrá el número de individuos que decidamos de antemano. Para obtener dicha población nos basta con encontrar aleatoriamente tantas permutaciones como sean necesarias y, entre estas, escogemos por sorteo unas cuantas. Supongamos que, en nuestro caso, la población inicial es de 6 individuos. Construimos dichos individuos aleatoriamente y obtenemos los siguientes:

{ABEFDC, ABCEFD, AEBCFD, ACDBEF, AEFCDB, ADCBFE}

Empezamos siempre en la A que es donde está el punto de partida y entendemos que, al final, hemos de volver a A.

--Una función de evaluación: Algún criterio que nos mida cómo de buenos son los elementos de esta población que hemos creado aleatoriamente, asignando a cada elemento un número que será la medida de su aptitud. En el ejemplo de las 6 ciudades, este número sería la longitud de cada una de las rutas, sumando las distancias entre elementos consecutivos de cada permutación: para ABEFDC, por ejemplo, medimos la distancia de A a B, le sumamos la distancia de B a E, de E a F, de F a D, de D a C y de C a A.

En este caso, cuanto menor sea la longitud total, mayor será la aptitud, porque buscamos soluciones con longitudes pequeñas.

--Un proceso de selección para cruces: Realizamos un sorteo entre los individuos de la población inicial, para cruzarlos por parejas, dando más papeletas a aquellos que tengan más aptitud. Es decir, los individuos con mayor aptitud tienen más probabilidades de ser seleccionados para ser cruzados con otros individuos. Eso es así en la vida real también... En nuestro ejemplo, de 6 individuos, vamos a elegir 3 parejas (podemos repetir individuo en más de una pareja, por ejemplo, si uno de los individuos es muy, muy apto).

Si una de las parejas elegidas es, por ejemplo, la formada por los individuosABCEFDy ACDBEF, tenemos que cruzarlos para obtener un nuevo individuo para la siguiente población.

Hay varios métodos para hacer esto, voy a proponer uno simple: hacemos otro sorteo y elegimos un número entre 2 y 4. Sale 3. Eso significa que al cruzar ABCEFDcon ACDBEF, vamos a obtener dos hijos: para el primero escogemos las 3 primeras ciudades de ABCEFD: ABCy el resto de las ciudades las recorremos, después de C,en el orden en el que aparecen en el otro progenitor, ACDBEF: después de C está D, después estaría B, pero como por Bya hemos pasado, nos la saltamos y vamos a Ey por último a F; por tanto, el primer hijo sería ABCDEF.

Ahora hacemos lo mismo empezando por ACDBEF y obtenemos el segundo hijo: ACDBEF(que, curiosamente, es igual que uno de sus padres, pero no nos preocupamos por ello).

Con este procedimiento tendríamos 2 hijos de cada una de las 3 parejas elegidas por sorteo, es decir, 6 nuevos individuos para volver a empezar y repetir el proceso si queremos mejorar la aptitud.

Pero, ¡ojo!, ahora viene un detalle muy importante. Ahora interviene un elemento esencial, sin él el método no funcionaría, sin él la naturaleza no habría obtenido los individuos que mejor se adaptan a su habitat: la mutación, las cadaunadas.

Mutaciones ocurren pocas y la mayoría son regresivas: dan peores individuos, pero, muy de vez en cuando, producen individuos mejor adaptados y sin ella el proceso darwiniano no tendría sentido. Así lo que hacemos es, una vez obtenidos los hijos, realizamos un nuevo sorteo pero tal que la probabilidad de ser mutado sea muy pequeña (digamos 1 entre 1000). Así, de cada 1000 individuos mutamos aproximadamente a 1. Supongamos que uno de los hijos que hemos obtenido en el proceso anterior ABCDEF sale mutante, ¿qué hacemos? Realizar otro sorteo (ya llevamos unos cuantos) y sacamos dos números entre el 2 y el 6, por ejemplo 3 y 5, pues intercambiamos las ciudades que aparecen en tercer y quinto lugar para obtener ABEDCF.

Se trata ahora de medir la aptitud de la nueva población, si nos satisface, paramos; en otro caso, repetimos el proceso.

Lo increíble de este tipo de algoritmos en el que se toman tantas decisiones aleatorias, con tantos sorteos, es que consiguen en muy pocos pasos, soluciones muy buenas. De hecho, existe un resultado matemático que nos asegura que, con este método, vamos a aproximarnos a la solución óptima tanto como queramos (cuantas más generaciones mejor) y que si algunos de los elementos no lo tenemos en cuenta puede que nunca nos aproximemos a dicha solución porque nos quedemos estancados en lo que se llama un óptimo local y nunca nos aproximemos al óptimo global que es lo que estamos buscando.

 

¿Y qué tiene que ver todo esto con las listas de consejos para usar Twitter, Facebook, Instagram, Flickr...?

Si todos seguimos las listas de consejos no estamos siguiendo un proceso evolutivo: nos estamos estancando en óptimos locales ya que hacen que todos los individuos se parezcan y eliminamos diversidad que es fundamental para obtener mejores elementos. En algún sentido se puede decir que el mestizaje es fundamental para la mejora de la población y que poblaciones muy endógamas (como las familias reales), suelen degenerar y dar individuos muy defectuosos.

Un consejo: mézclense y si alguna vez se les ocurre algo que a los demás les parece una auténtica locura, recuerden lo que decía Gaudi: “Mis ideas son de una lógica indiscutible; lo único que me hace dudar es que no hayan sido aplicadas anteriormente.” No duden.