DANDO LA VUELTA AL EFECTO MARIPOSA
Del caos al orden: sí se puede
Seguro que han oído hablar de la mariposa que con su aleteo desencadena un tifón en la otra punta del mundo, es decir, de cómo un pequeño desorden puede generar un gran caos. Hoy les contamos que al revés también sucede: se puede generar orden desde el caos.
Publicidad
Es sabido que hay sistemas caóticos en los que una pequeña variación de las condiciones iniciales motiva una enorme variación del resultado final. Es la famosa mariposa del amazonas cuyo aleteo puede llegar a provocar un tifón en el Pacífico.
Eso es debido a que las ecuaciones que rigen la climatología presentan de forma muy acusada se comportamiento caótico, lo cual quiere decir que una minúscula variación en las condiciones iniciales (esa variación que puede causar el aleteo de una mariposa) podría llegar a cambiar tan drásticamente el resultado final (el resultado de aplicar las ecuaciones en el Pacífico al cabo de unas cuantas semanas) como para desencadenar o no un tifón.
Sin embargo, hay otros sistemas enormemente útiles que verifican el fenómeno contrario: partiendo de una situación caótica se llega siempre al mismo final (y ordenado). Ello permite encontrar la solución computacional de problemas que, en otro caso, sería imposible de obtener.
Así, cuando diversos métodos computacionales -los algoritmos genéticos por ejemplo, de los que ya hemos hablado aquí- tratan de encontrar el individuo que optimiza una cierta función, parten de una población inicial escogida al azar que no presenta ningún orden específico y siguiendo ciertas reglas, se puede garantizar que se van acercando tanto como queramos a la solución óptima del problema.
Tal y como hemos dicho, este tipo de algoritmos -que no son sólo genéticos- permiten partir de una posición inicial que no presenta ningún tipo de orden -elementos de la población escogidos al azar- y por la aplicación sucesiva de ciertas reglas -en las cuales, en el caso de los algoritmos genéticos, también juega un papel importante el azar- se llega a unos elementos concretos de la población.
Podríamos decir entonces que hemos pasado del caos al orden.
Hoy queremos comentar aquí un ejemplo del camino del caos al orden que, en principio, no parece que pueda ser de gran utilidad (aunque eso nunca se sabe) pero sí es de gran belleza:
Has de seguir las siguientes reglas:
1) Toma tantos puntos como quieras y donde quieras en el plano.
2) Recorre dichos puntos en el orden que se te antoje hasta terminar de nuevo en el que empezaste (dibujando el segmento correspondiente en cada paso).
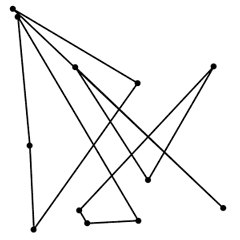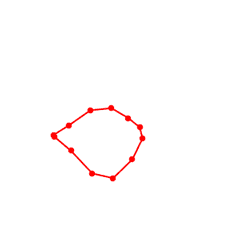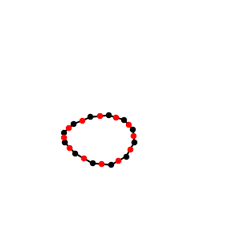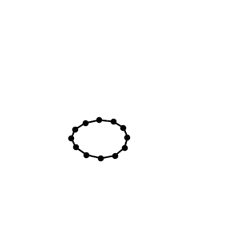
Si has seguido las reglas 1 y 2 habrás obtenido un polígono -aunque puede tener muchos cruces los matemáticos seguimos llamando a eso un polígono-. Y dicho polígono está claro que no presenta ningún tipo de orden. Esta es nuestra situación inicial desordenada o caótica.
Ahora, como en el caso de los algoritmos genéticos, vamos a dar unas reglas muy sencillas para que dicho polígono evolucione. Dichas reglas son:
3) Dibuja los puntos medios de los segmentos obtenidos en el punto 2).
4) Une los puntos medios obtenidos en 3) siguiendo el mismo orden que diste en 2)
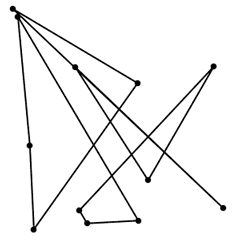
Así supongamos que dibujamos unos puntos y los unimos en cualquier orden (instrucciones 1 y 2) y obtenemos este polígono:
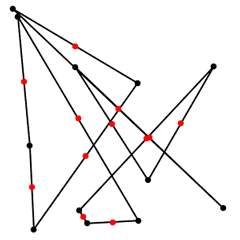
Ahora consideramos los puntos medios de cada segmento:
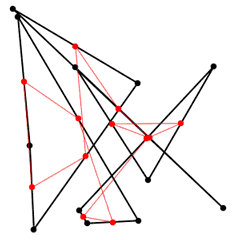
Y unimos dichos puntos medios en el mismo orden:
Y obtenemos este polígono:
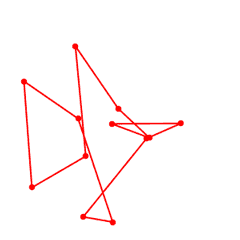
Y volvemos a aplicar el mismo proceso una y otra vez.
Como se puede observar, el último polígono tiene menos cruces que el primero. Una pregunta lógica sería si al aplicar repetidas veces este proceso se obtendría un polígono sin cruces La respuesta, sorprendentemente, es sí: al aplicar las reglas descritas siempre se obtiene un polígono sin cruces, pero no sólo eso (y aquí viene la magia): se obtiene siempre una elipse
En este gif se puede ver la evolución del polígono que hemos tomado como ejemplo:
Este hecho sorprendente lo han probado dos miembros de Cornell University (Adam N. Elmachtoub y Charles F. van Loan) y si alguien está interesado, su artículo está disponible aquí.
También se puede jugar un poco con este resultado en esta página en la que se generan polígonos aleatorios y se le aplican estas reglas.
Ya ven, del caos al orden. Se puede. Lo digo por lo de las elecciones generales que tenemos este mes.
Publicidad