PROBLEMAS COTIDIANOS CON SOLUCIÓN CIENTÍFICA
Cómo aparcar el coche usando las matemáticas
Posiblemente alguna vez has tenido que aparcar en línea en una calle estrecha y has desistido porque no tenías espacio suficiente para girar en la maniobra ¿Cuál es el espacio mínimo requerido para girar un coche? ¿Y una varilla de un metro? A veces, preguntas tan cotidianas y simples como estas han dado lugar a grandes investigaciones en matemáticas.

Publicidad
Estoy casi segura de que han oído a alguien utilizar la expresión "dar un giro de 360º" como analogía de cambio radical en su vida, por ejemplo. Estoy casi segura también de que han sonreído con ternura sabiendo que un giro de 360º no es ningún cambio radical porque se trata de una vuelta completa y dar semejante giro nos deja donde empezamos. Es decir, que la expresión de marras se puede usar más como analogía de la pasividad y el inmovilismo que como síntoma de cambio radical.
Sin embargo, en otras situaciones querer dar un giro de 360º puede dar pie a una extensa investigación en matemáticas. Por ejemplo, imaginen que tienen una aguja (una varilla) de un metro de longitud, ¿cuál es el área mínima que necesito para girarla?
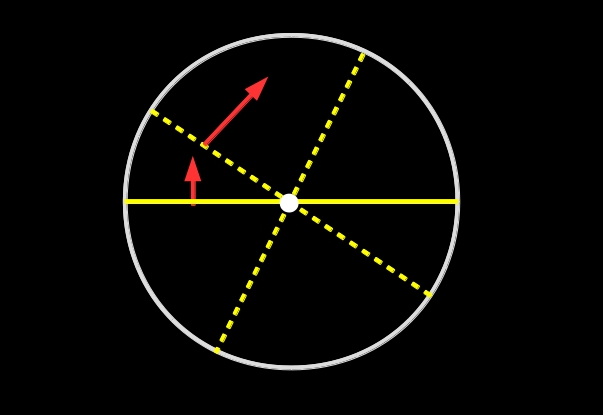
A poco que uno lo piensa, llega a la conclusión de que, claro, en un círculo de diámetro 1 metro, es posible girarla.
Pero, ¿se puede hacer en un recinto más pequeño? Pues sí, también. Basta con un triángulo equilátero de altura 1 metro y con usar el mismo tipo de 'maniobras' que usamos para aparcar nuestro coche, girar hasta donde se pueda, avanzar o retroceder, volver a girar...
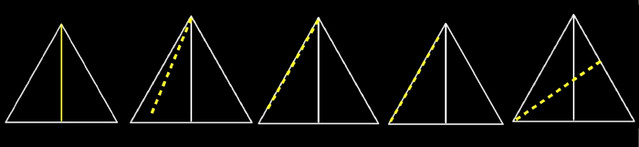
Nos fijamos en una de las alturas del triángulo (esa será la varilla, en amarillo en el dibujo), la giramos un poco, la llevamos sobre uno de los lados del triángulo, la bajamos hasta el otro vértice del triángulo (el inferior izquierdo en la figura) y la giramos hasta tocar el lado opuesto del triángulo
¿Se puede hacer en un recinto más pequeño? Según Soichi Kakeya, sí.
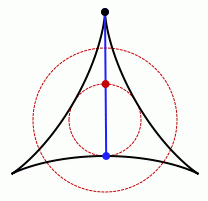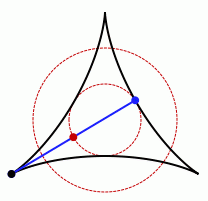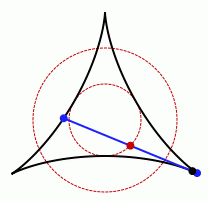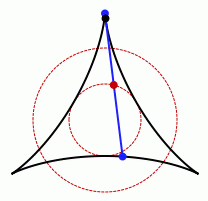
Este matemático japonés defiende que el recinto de menor área en el que se puede girar una varilla de un metro (permitiendo desplazamientos como en el parking) es un una figura conocida como deltoide, como el que aparece en la siguiente animación:
Si la varilla mide 1 metro, el diámetro de la circunferencia dibujada por el punto medio de la misma, en rojo en la figura es de 50 centímetros, la mitad de la longitud de la varilla.
Desafortunadamente, nuestro colega japonés estaba equivocado. No obstante, este problema fue bautizado como el problema de Kakeya puesto que fue él quien lo propuso.
Efectivamente, hay recintos más pequeños que el deltoide en los que puede girar la aguja. De hecho, podemos encontrar recintos del área que queramos, por muy, muy pequeña que esta sea, en los que pueda girar la varilla. Sí, ha leído bien, podemos encontrar recintos de áreas infinitamente pequeñas, cercanas a 0, en los que girar nuestra aguja.
A estos recintos se les llama, en un alarde de imaginación, conjuntos de Kakeya ¿Qué? ¿Que no? Pues sí, lo demostró el matemático ruso Abram Samoilovitch Besicovitch. Elija un número (positivo, claro), el más pequeñito que se le ocurra, y Besicovitch le construye un recinto con una superficie menor que su número elegido y en el que puede girar 360º una varilla de 1 metro de longitud. En realidad, la propiedad que tienen los conjuntos descritos por Besicovitch es que en ellos podemos colocar una varilla de un metro, por ejemplo, en cualquier dirección. Pero a partir de estos, de los conjuntos de Besicovitch, se pueden construir conjuntos de Kakeya.
¿Cómo lo hace? Uno de los métodos más conocidos para ello es el propuesto por otro matemático, esta vez alemán, Oskar Perron en un trabajo de 1928, en el que simplifica la propuesta del ruso para ello. La construcción de Perron, conocida como el árbol de Perron, consiste en partir de un triángulo equilátero de altura un metro y dividirlo en un número suficiente de triángulos iguales, para luego superponer convenientemente dichos triángulos, de forma que dentro de la figura así obtenida quepa una varilla de un metro de longitud en cualquier dirección. Cuantos más divisiones hagamos del triángulo original, menos área tendrá la figura (el árbol) resultante de las superposiciones.
Ahora solo tenemos que rotar y combinar los árboles de Perron para conseguir recintos de Besicovitch tan maravillosos como este:
Ahora, igual que para aparcar en un sitio estrecho, se trata de maniobrar con la varilla girando, avanzando y retrocediendo...
Este tipo de problemas, que nacieron casi como divertimentos matemáticos, tienen infinidad de aplicaciones en estadística, matemática discreta, combinatoria, ecuaciones en derivadas parciales... Les dejo este trabajo de Terence Tao que explica algunas de ellas.
Seguimos otro día. Ya no tienen excusa para no aparcar en calles estrechas, solo necesitan paciencia. Y dirección asistida, claro.
Publicidad