Cómo saber por dónde van los tiros (literalmente)

Imaginen que estamos en la guerra y nuestras trincheras están siendo castigadas duramente por fuego de artillería enemiga. Creo que todos coincidiremos en que sería muy deseable saber desde dónde se nos dispara: con esa información, podríamos intentar neutralizar sus cañones y dormir más tranquilos.

Tradicionalmente se había confiado esta tarea a vigilantes que trataban de distinguir desde dónde provenía el fuego enemigo usando dos micrófonos (situados a una cierta distancia entre ellos) y midiendo el tiempo que tardaba el sonido en llegar de uno a otro.

Así, cuando estos señalaban un fogonazo proveniente del disparo de un cañón se podía determinar la dirección en la que estaba dicha pieza de artillería, pero no la distancia, algo para lo que se trataba de discernir cuánto tardaba el sonido en llegar.

Pero, como cabe suponer, en mitad de una batalla era casi imposible determinar qué cañón en concreto había producido el sonido que se estaba escuchando, así que era necesario que dos vigías situados a una distancia conocida identificaran a la misma pieza, algo muy improbable. Un lío, vamos.

Una idea renovadora

Parece que este era el método que usaban todavía los alemanes en la Primera Guerra Mundial, por ejemplo. Pero los aliados lo descartaron pronto e implementaron un método que, basado en la geometría clásica, permitía determinar con mucha precisión el origen de los disparos. Para ello fue necesario, eso sí, disponer de una tecnología que no existía en conflictos anteriores.

En este caso también se necesitaban varios puestos, que registraban el sonido, y de lo único que se trataba era de mandar la información grabada en cada puesto a un procesador central que con toda la información determinaba de dónde procedía cada cañonazo.

En realidad, la idea se parece mucho a la que usa el GPS para ubicarnos en la Tierra, pero de forma un poco más simple. El primer paso era identificar cada cañonazo concreto -se supone que cada cañón producía un sonido más o menos distinguible- y, a partir de ese momento, resolver un problema de geometría por métodos conocidos desde la época de la Grecia clásica.

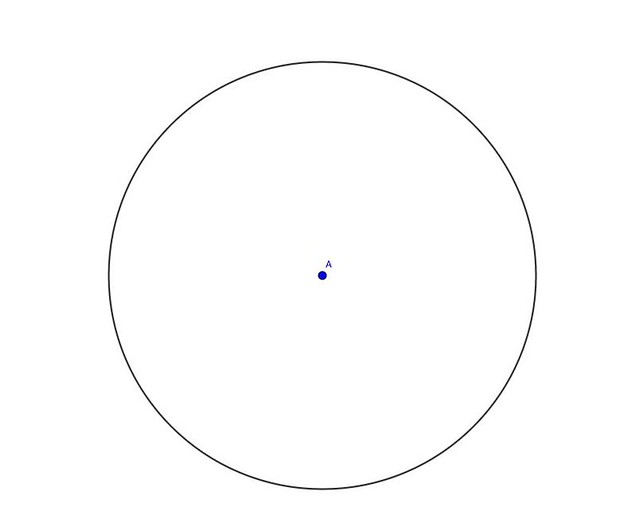
Si dispusiéramos sólo de un micrófono que registrara el sonido sería imposible saber dónde está el cañón enemigo, incluso aunque supiéramos cuánto ha tardado el sonido en llegar hasta nuestro micrófono, dato que desconocemos, puesto que podría estar en cualquier lugar de esta circunferencia:

En términos matemáticos: si las coordenadas del punto A (donde está el micrófono) son (a₁,a₂) y sabemos que el radio de la circunferencia es R (distancia a la que suponemos que está el cañón por lo que ha tardado el sonido), el cañón podría estar en cualquiera de los puntos de coordenadas (x,y) que verifiquen que:

Ésta es la ecuación de la circunferencia centrada en (a₁,a₂) y de radio R, pero no sabemos ni cuánto valen ni x, ni y, ni R. Esta es una diferencia con el sistema GPS donde sí se conoce esta R.

Así que tenemos una ecuación y tres incógnitas, y de ahí las infinitas soluciones. Hay que buscar otro micrófono.

Si tuviéramos dos micrófonos -situado en el punto B de coordenadas (b₁,b₂)- la situación mejoraría, pero seguiríamos sin saber con precisión el punto exacto desde el que provienen los disparos. En este caso, tendríamos una nueva ecuación:

En ella (b₁,b₂) serían, como hemos dicho, las coordenadas del segundo micrófono y Mla distancia recorrida por el sonido en el tiempo transcurrido desde que el micrófono 1 (en A) recibe la señal hasta que la recibe el micrófono 2 (en B).

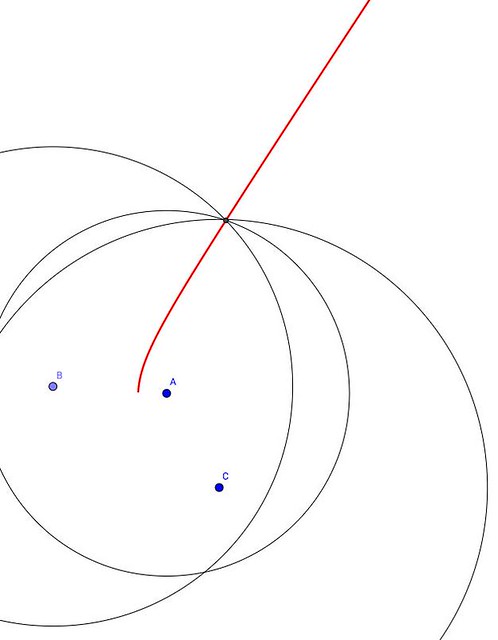
Tenemos entonces, tres incógnitas (x, y y R ) y dos ecuaciones. Con estos datos, todos los puntos de la línea roja en este dibujo podrían constituir una localización factible de la pieza enemiga:

La solución es evidente: necesitamos tres micrófonos receptores.

Pues nada, ponemos un tercer micrófono en un punto C de coordenadas (c₁,c₂) y llamamos N a la distancia recorrida por el sonido en el tiempo transcurrido desde que el micrófono 1 (en A) recibe la señal hasta que la recibe el micrófono 3 (en C).

Con ello tendríamos tres ecuaciones con tres incógnitas y, aunque son ecuaciones al cuadrado, en este caso sí se pueden resolver y obtener una única solución. Al representarlo gráficamente se determinaría un único punto

Naturalmente, el procedimiento tenía sus dificultades: aún había que aislar el sonido de un único cañón entre decenas de ellos y, además, el análisis tenía que ser muy preciso.

Hoy en día se utilizan otros métodos que implican el uso de satélites o de rádares, pero todavía algunos ejércitos utilizan variaciones de este sistema como método principal para detección de la artillería enemiga.

Como decíamos al principio, es mucho más fácil saber por dónde van los tiros en la guerra que en nuestro Congreso, por ejemplo. En este no sirve de mucho saber geometría.