Qué tienen en común el cine, Wall Street, tu cumpleaños y las matemáticas

Gran parte de lo que ocurre en todo el mundo es decidido por algunos de los cerebros que controlan Wall Street. Supongo que para muchos ser uno de los lobos que trabajan allí debe ser llegar a una especie de máximo en sus carreras. Naturalmente, las preguntas que te formulan para poder entrar en una de las empresas punteras suelen ser bastante duras y muchas de ellas, cómo no, tienen un alto contenido matemático.

Como les contaba en la entradilla, el otro día en la cola del cine me acordé de ésta, formulada por una de las compañías más grandes y poderosas: Morgan Stanley.

Un grupo de personas está en la cola de la taquilla de un cine. El dueño del local dice que cada cual puede cambiar su posición pero que el primero en la cola que tenga alguien delante de él con el que coincida el día de su cumpleaños podrá entrar gratis. Si puedes elegir ¿dónde te situarías?

Este interesante problema nos recuerda, en algún sentido, a otros dos como son la paradoja del cumpleaños y la elección de secretaria.

Recordemos la paradoja del cumpleaños: en un grupo de N personas, ¿qué probabilidad existe de que para al menos dos de ellas coincida su cumpleaños? Para calcular dicha probabilidad es mucho más sencillo calcular su complementario, esto es: ¿cuál es la probabilidad de que no coincida ninguna fecha de cumpleaños?

Así si hay dos personas (N=2), la probabilidad de que no coincidan sus cumpleaños (eliminemos años bisiestos) es de 364/365, casi 1. Recordemos que la probabilidad es un número entre 0 (seguro que no ocurre ese hecho) y 1 (seguro que ocurre). Para tres personas, hay que multiplicar probabilidades y obtenemos (364x363)/(365x365).

Una vez encontradas estas probabilidades de que ningún cumpleaños coincida, para calcular su complementario basta con restar dicha cantidad a 1. Si llamamos P(N) a la probabilidad de que en un grupo de N personas al menos dos de ellas tengan la misma fecha de cumpleaños, obtenemos que P(1)=0, P(2)=1-(364/365), P(3)=1-(364x363)/(365x365)...

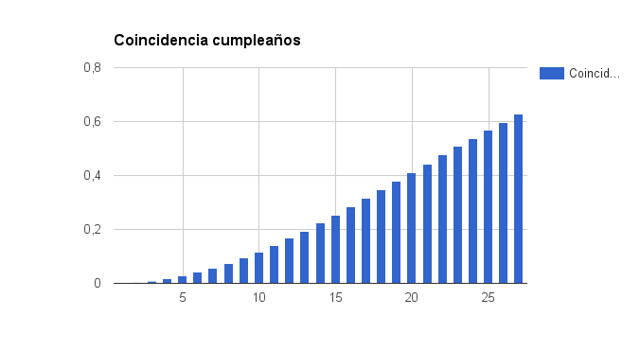
El gráfico de estas probabilidades es:

Y sí, es muy llamativo que con solo 25 personas la probabilidad de que dos de ellas cumplan años el mismo día sea superior al 50%, de ahí lo de paradoja.

Pero no estamos buscando esta probabilidad. Para ganar la entrada gratis necesitamos que al ponernos en nuestra posición en la cola, se repita un cumpleaños y que delante nuestro no se repita ninguno, con lo que estaríamos garantizando que el que se repita primero sea el nuestro. Así que la probabilidad que buscamos para cada posición N es de P(N)-P(N-1), siendo P(N) la probabilidad de que se repita algún cumpleaños entre los N primeros y P(N-1) la probabilidad de que se repita un cumpleaños antes de mi posición, que es la N.

Haciendo algunas cuentas y con ayuda de la tabla anterior podemos construir esa función y nos da:

Pues bien, se puede comprobar que el mejor valor se obtiene si nos colocamos en la posición 20, en la que se obtiene un valor de 0,03231985755. No es mucho, pero es lo mejor. En cualquier caso, no estamos interesado en conseguir una entrada gratis para el cine sino en ser un lobo de Wall Street o un jedi de al bolsa.

Estoy casi segura de que las matemáticas serían tan útiles como la fuerza para un jedi o, mejor aún, que las matemáticas son la fuerza. En cualquier caso, mucho que aprender todavía tenemos.