Curvas de Bézier: la matemática tras los cuadros de Picasso

La primera y razonable respuesta a la pregunta de qué tienen que ver Picasso, los coches y las matemáticas podría ser 'nada'. Sin embargo,  existe una relación bastante curiosa y está relacionada con una frase que se repite muchas veces cuando se intenta rechazar el mérito de parte de la pintura de Picasso: “eso lo puede dibujar cualquiera, hasta un niño”. Traigan a un niño, como diría el señor Marx.

No es este el lugar para refutar semejante simpleza. Es más, voy a ir un paso más allá: algunos de los dibujos de Picasso son tan simples que hasta un matemático podría hacerlos. Toma ya.

Efectivamente, tal y como se señala en esta página, gran parte de los dibujos del ilustre malagueño pueden reproducidos usando solo curvas de Bézier, que son un objeto matemático que casi seguro que has visto y usado alguna vez, aunque no seas consciente de ello.

Las curvas de Bézier fueron desarrolladas por el ingeniero francés Pierre Bézier, que  trabajó para la Citroën y para la Renault.  A principio de los '60 desarrolló dicha herramienta y la usó con profusión en el diseño de piezas de automóviles.  Posteriormente fueron adoptadas también por la industria aeronáutica y en la actualidad casi cualquier programa informático que tenga que ver con gráficos  las tiene como herramienta.

Hablamos de esa herramienta de diseño que sirve para dibujar curvas y que nunca nos las dibuja exactamente como queremos. Bueno, el primer y último punto sí, pero la zona intermedia siempre nos sorprende, incluso a veces nos cabrea.

Vamos a tratar de ver cómo funciona y cómo se trazan las curvas de Bézier para que no nos coja desprevenidos la próxima vez:

Una curva de Bézier depende siempre de tres o más puntos que son los llamados puntos de control. Nos los  tenemos que imaginar como el camino descrito por un objeto que va desde el primer punto hasta el último, pero que se siente 'atraído' por los puntos intermedios.

Aunque en la mayoría de las aplicaciones se utilizan cuatro puntos de control, creo que deberíamos empezar por las curvas que solo utilizan tres.

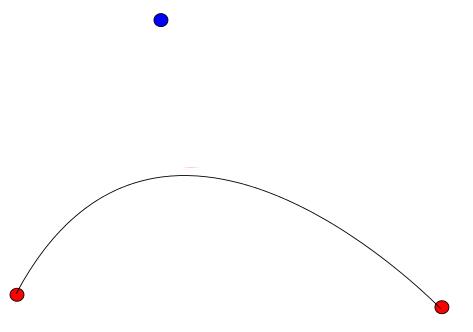
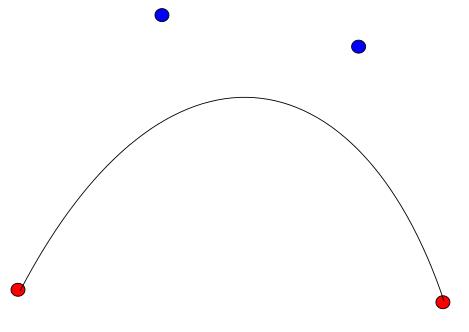
Abrimos nuestra aplicación de dibujo favorita, seleccionamos la herramienta que dibuja curvas (de Bézier) y marcamos con el ratón un punto, arrastramos hasta otro y soltamos: hemos creado nuestro segundo punto de control. Ahora nos movemos hasta un tercer punto en el que hacemos doble click para terminar de dibujar la curva. Estos son nuestros tres puntos:

En contra de lo que cabría esperar, el programa nos dibuja esta curva:

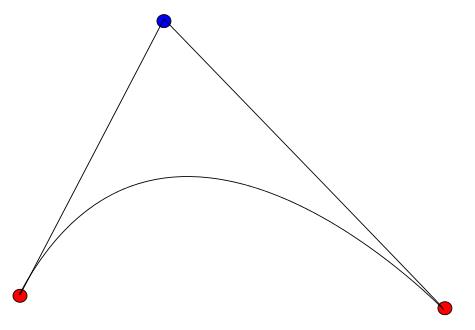
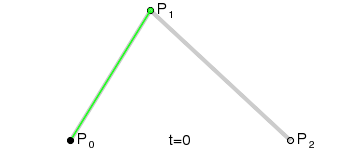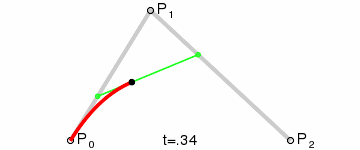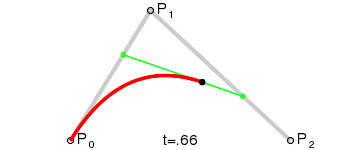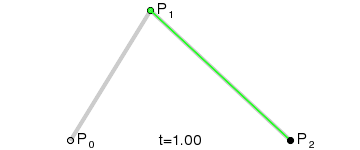
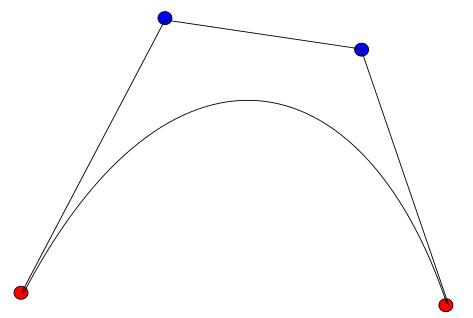
Pero, ¿por qué?  Para entenderlo haremos lo siguiente: unimos con una línea el primer punto (el rojo más a la izquierda) con el intermedio (azul)  y este con el final(rojo):

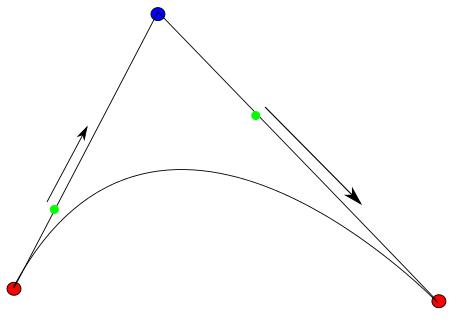
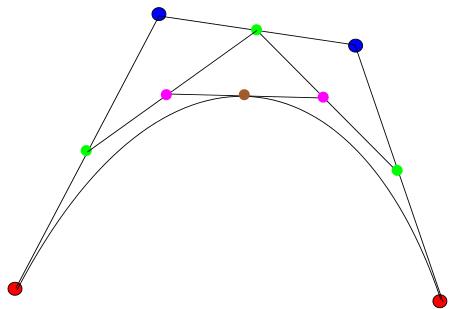
Pensemos ahora que un punto verde se pone a caminar desde el primer punto rojo  hasta el intermedio y otro, que sale al mismo tiempo desde el punto azul, se pone a caminar desde dicho punto azul hasta el último rojo, pero los dos puntos verdes no caminan a la misma velocidad, sino que ajustan sus velocidades para llegar ambos a las vez a sus respectivos destinos:

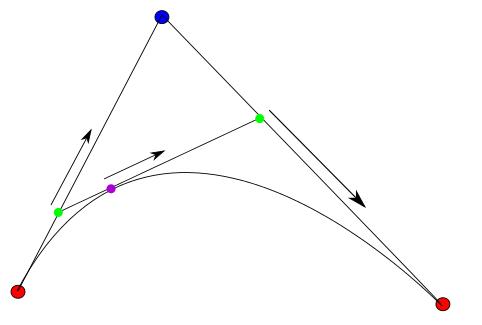
Unimos ahora  ambos puntos verdes con un elástico (elástico porque la distancia entre ellos varía según se mueven) y en dicho elástico viaja un punto morado que va desde un punto verde hasta el otro y que también ajusta su velocidad para empezar su recorrido a la vez que ambos verdes y terminar con ellos:

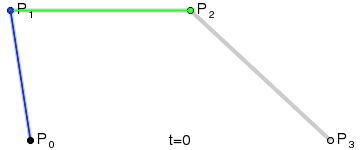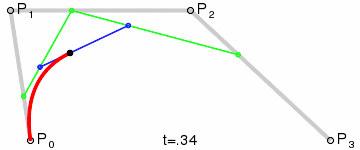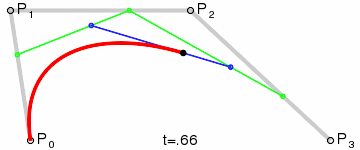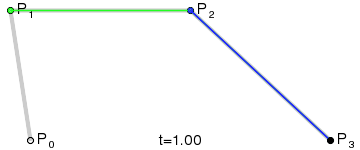
Pues si dibujamos la ruta que sigue dicho punto morado, obtenemos exactamente la curva de Bézier definida por los puntos rojos y el azul. Aquí se puede ver todo el proceso con una animación:

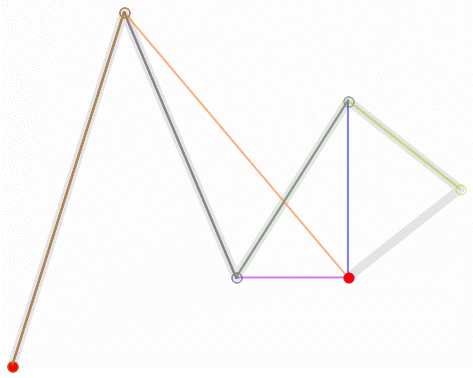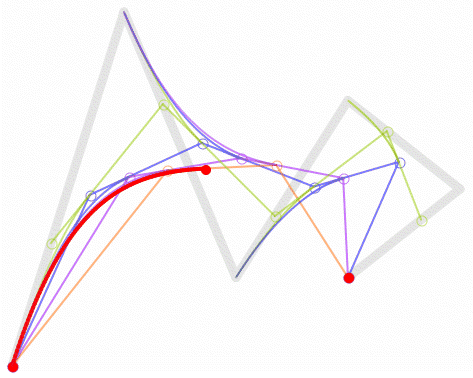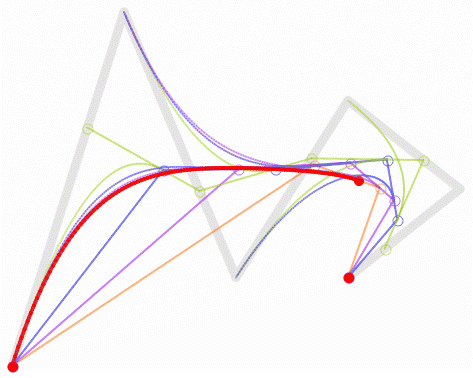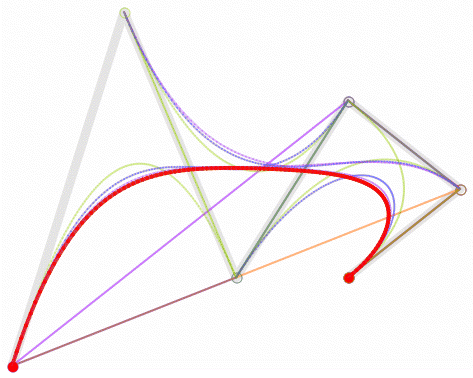
¿Y si tenemos cuatro puntos de control? El proceso es similar: empezamos en un punto, arrastramos hasta otro, nos movemos hasta el último y arrastramos para crear el 'tirador' (segundo punto intermedio). Los cuatro puntos son estos:

Y el resultado es esta 'carita triste':

¿Cómo se llega a ella? Pues por un procedimiento similar al descrito antes: unimos el primer punto con el segundo, este con el siguiente y el tercero con el último:

Y ahora tres puntos verdes se ponen a caminar por cada uno de los tres segmentos de tal forma que salgan y lleguen a la vez. Entre el primer y el segundo punto verde llevan un elástico por el que camina un punto morado y entre el segundo y el tercero hacemos igual, y ahora le damos otro elástico que va entre ambos puntos morados y por dicho elástico camina un punto marrón que será el que trace la curva:

De nuevo recurrimos a una animación para verlo:

Y ya está.  Bueno, ya está no, pueden seguir añadiendo puntos de control y obtener curvas de Bézier tan monas como esta:

La próxima vez que intenten usar una curva de Bézier en su ordenador y no les salga el dibujo esperado, piensen que a lo mejor no son tan simples los dibujos de Picasso como algunos creen