UNA DE PRUEBAS MATEMÁTICAS
Exámenes difíciles… y xenófobos
¿Se pueden usar las matemáticas con fines xenófobos? La respuesta es que sí porque ya se hizo en Rusia no hace tanto proponiendo ejercicios aparentemente muy difíciles a los judíos. Aparentemente, porque no lo eran tanto como no lo son esos que últimamente se hacen virales en internet.

Publicidad
Durante las décadas de los '70 y los '80 del siglo pasado la Universidad Estatal de Moscú disponía de unos métodos una 'mijita' xenófobos para evitar la entrada de estudiantes judíos u otras personas indeseadas en sus aulas: los problemas judíos. Estos problemas son conocidos también con los intuitivos nombres de "ataúdes" o"asesinos". Y sí, muchos aspirantes judíos a la citada universidad tuvieron que enterrar sus aspiraciones en alguno de estos ataúdes hechos no de madera de pino, sino de perversidad matemática.
En su reciente libro 'Amor y matemáticas' Edward Frenkel relata cómo él mismo en 1984 sufrió esa xenofobia cuando trató de ingresar en dicha universidad. De hecho, es uno de los ejemplos que otro matemático, Mark Saul, utiliza en este artículo de 1999 para denunciar esta práctica de la universidad rusa. Sobre este mismo asunto se publicó el libro 'You failed your math test, Comrade Einstein: adventures y misadventures of young mathematicians' en el que el matemático Ilan Vardi presenta y compara los problemas mencionados con los de la Olimpiada Matemática del año 2000. Incluye, además, un ensayo llamado 'El genocidio intelectual' explicando el trasfondo histórico de esta práctica llevada a cabo en la URSS.
La historia de los problemas judíos también tiene su heroína, Bella Abramovna Subbotovskaya, que ante esta situación de injusticia con los judíos fundó en 1978 con ayuda de otros colegas la Universidad del Pueblo Judío, cuyas primeras clases se impartieron en el propio apartamento de Subbotovskaya. Sus amigos la describen como fuerte, enérgica y reivindicativa, al mismo tiempo que cálida, bondadosa y optimista. Todos resaltan su enorme determinación.
Pues bien, Bella murió de forma extraña cuando sólo tenía 44 años. “Los días previos a su muerte había sido convocada en varias ocasiones por la KGB y sometida a interrogatorios. El crimen sobre el que fue interrogada fue la creación de la Universidad del Pueblo Judío”, escribió George G. Szpiro en este artículo de 2007.
Lo cierto es que, para evitar reclamaciones e impugnaciones al proceso, todos estos problemas tenían (tienen) una solución muy sencilla, pero a la vez difícil de encontrar, puesto que era necesaria una idea feliz que te condujera trivialmente a resolverlo. De esta manera, nadie podía alegar que eran ejercicios irresolubles o muy complicados.
Los 'virales' actuales
Esto fue en Rusia y en el siglo pasado (bueno, hace menos de 50 años) pero últimamente seguro que les ha llegado a través de las redes sociales algún examen ‘super’ difícil que ha sido propuesto en algún lugar del mundo, ¿no? Pues no, la mayoría de ellos no lo son y el hecho de que se hagan virales como problemas complicados dice mucho del nivel en matemáticas en nuestro país.
Los dos problemas que más revuelo han causado en las redes sociales y ciertos medios de comunicación son el del cocodrilo y la cebra preguntado en Escocia y el de la moneda de 50 centavos de Australia.
Del primero de ellos ya se ha hecho eco Gaussianos y creo que deja bastante claro que cualquier persona que sepa lo elemental de derivadas (no olvidemos que son alumnos que van a entrar en la universidad en una carrera técnica o de ciencias) puede resolverlo. En fin…
Aún más sangrante me parece el caso del problema de la moneda de 50 centavos australiana. También es un examen de ingreso en la universidad y se plantea la siguiente cuestión:
Aunque supongo que está bastante claro, lo traduzco:
Una moneda de 50 centavos tiene 12 lados de la misma longitud. Dos de dichas monedas se sitúan una junto a la otra de tal forma que se tocan a través de un lado (de cada una de ellas). ¿Cuánto vale el ángulo marcado con una X en la figura?
Voy a contar cómo se soluciona este problema que tanto revuelo ha causado en las redes sociales y que algunos medios han calificado como muy difícil, pero antes me gustaría que el lector lo pensara un poco.
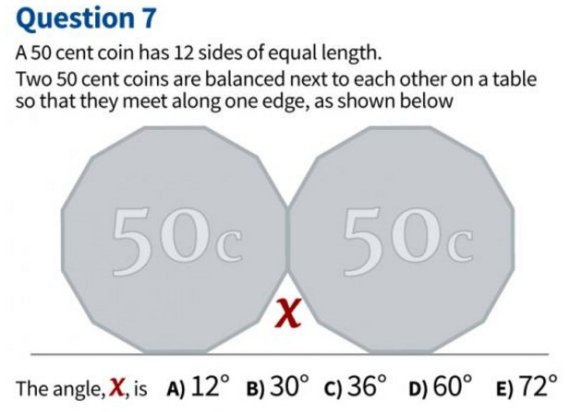
Como hemos dicho, se trata de saber cuánto es el ángulo que aparece dibujado en rojo en la figura:
Ese ángulo X, junto con el ángulo A que marcamos en azul, ha de sumar 360º:
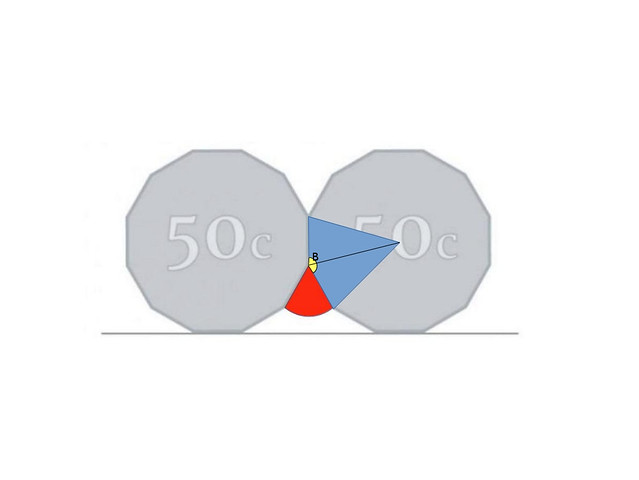
Vamos a tratar de averiguar A. Evidentemente, A es el doble de su parte que cae enteramente en una de las dos monedas (al que llamaremos B):
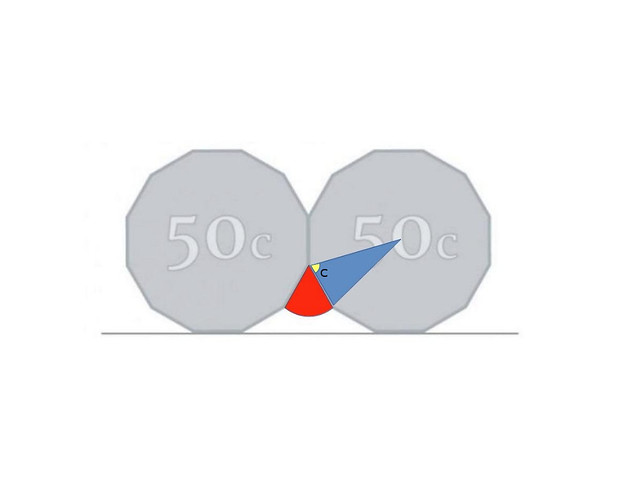
Pero B, a su vez, es el doble del ángulo C, que es la parte de B que cae dentro de uno dos los dos triángulos equiláteros en los que dividimos el cuadrilátero azul anterior:
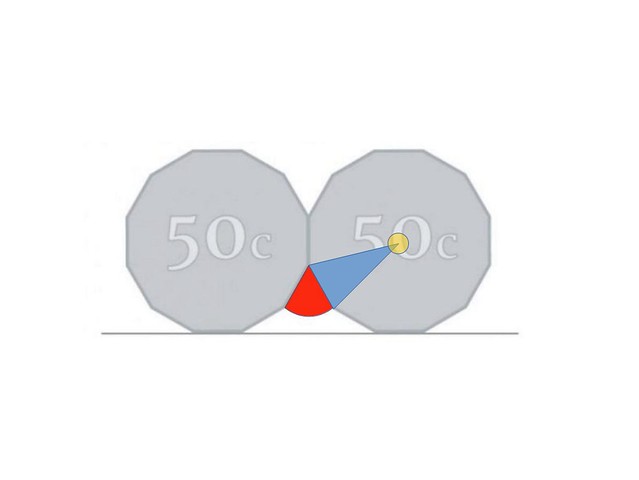
Pero C es muy fácil de calcular porque sabemos como dato que 12 triángulos como el que tenemos azul rellenan toda la moneda (que tiene 12 caras) y, por lo tanto, en el triángulo azul, el ángulo superior, el que está pegado al centro de la moneda, abarca 360º/12=30º
Ahora aplicamos casi el único concepto que tienen que saberse los aspirantes a universitarios australianos (y que debería saber todo el mundo, porque es cultura general): que la suma de los ángulos de un triángulo son siempre 180º. Así que C+C+30=180º, luego C=75º. Volvemos hacia atrás y B=150º, por lo tanto X=360º-2x150º=60º y 60º era una de las opciones que se nos presentaban.
Realmente pienso que no solo no es difícil, sino que es muy fácil para unos aspirantes a entrar en la universidad en carreras de ciencias o tecnológicas. Solo se ha pedido pensar un poco, muy poco, y poseer un conocimiento realmente elemental de las propiedades de los triángulos.
Lo que sí parece cada vez más complicado es que nos demos cuenta de que la ciencia también es cultura, pero seguiremos peleando hasta que nos enteremos todos
Publicidad