Mucha informática, pero las raíces cuadradas, a mano...

A todo cerdo le llega su San Martín y a todo padre o tutor le llega el momento en el que uno de sus vástagos le pide ayuda para calcular una raíz cuadrada a mano. Francamente, querida, siendo doctora en matemáticas, no he vuelto a necesitar calcular una raíz cuadrada a mano desde que me lo enseñaron en el colegio. Y claro, no me acordaba. Me puse a mirar el algoritmo que traía mi hijo para el citado cálculo y era exactamente el mismo que me enseñaron a mí: horrible y tedioso.

Por una parte, como he dicho, me parece que en los tiempos que corren y con la tecnología que tenemos a nuestra alcance, se debería insistir más en el planteamiento y resolución de problemas, para lo que es necesaria la intuición y la capacidad de razonamiento que no tienen las máquinas, y dejarle estos cálculos mecánicos a éstas. Pero, bueno, si siguen insistiendo en que hay que saber calcular a mano una raíz cuadrada, ¿por qué hacerlo con ese viejo algoritmo tan horroroso? Si se puede hacer de forma mucho más intuitiva y divertida. Sí, he dicho divertida, ¿qué pasa?

Déjenme que les cuente un resultado matemático sencillo e intuitivo: el teorema de Bolzano. Este teorema, de principios del siglo XIX, nos asegura que si queremos dibujar una curva sin levantar el lápiz del papel (eso es una función continua) y empezamos a dibujar encima del eje de las abscisas (el eje horizontal, el de las x) y terminamos debajo (o al revés) no hay más remedio que atravesar, al menos, una vez el eje. O más de una, como en la figura siguiente:

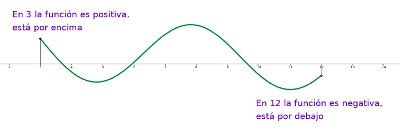
Yo siempre digo que desafío a Bolzano haciendo zapping porque paso del 4 al 6 de mi mando sin pasar por el 5. Pero hay incluso quien lo desafía con ascensores.

Ya sé, es un chiste viejo, pero me hace gracia. Volvamos a las matemáticas, ¿qué tiene que ver Bolzano con calcular una raíz cuadrada? Ya verán. Si nos piden calcular, a mano, la raíz cuadrada de 247, lo que nos están pidiendo es resolver la ecuación:

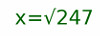
O lo que es lo mismo, si elevamos al cuadrado en ambos miembros:

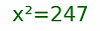
Esto es, queremos los valores de x que cumplen que:

Ya está aquí Bolzano. Queremos los valores de x que hacen que x²-247 valga 0. Como x²-247 es una función continua, créanme, solo hay que encontrar un valor para el que x²-247 sea positivo (esté por encima) y otro valor para el que x²-247 sea negativo (esté por debajo), nuestro sospechoso, la raíz cuadrada de 247 estará escondida entre ellos, solo hay que ir a acorralarlo y encontrarlo.

De hecho, en realidad, hay dos valores para la raíz cuadrada de 247, uno negativo y otro positivo, como para la raíz cuadrada de 4, tenemos -2 y 2; vamos a buscar el positivo, para el otro solo tendremos que plantarle un signo menos delante.

Por lo tanto, lo que en realidad buscamos, es un número que al cuadrado sea menor que 247 y otro número, que al cuadrado sea mayor que 247 sea mayor que 247, y el nuestro, estará escondido en medio. Ya, ya sé que esto se puede intuir sin conocer el teorema de Bolzano, pero así es más riguroso.

Seguimos ¿Qué número puede ser la raíz de 247? Se trata de usar eso, la intuición: 10 x 10 son 100, es muy poco… 20 x 20 son 400, eso es mucho …15 x 15 es, a ver, 15 x 10 son 150 más 15 x 5 que son 5 x 5 x 3…75. Es decir, 15 por 15 es 225… Es poco también, pero nos sirve para empezar.

Así que 15 no es la raíz cuadrada de 247, vale, pero dividimos 247 entre 15 y nos sale 16,466 (nos quedamos con tres decimales, por ejemplo). Efectivamente, 16,466 al cuadrado es mayor que 247 (se comprueba con la calculadora, mejor que a mano). Eso significa, que la raíz cuadrada de 247 está entre 15 y 16,466. Como no sabemos dónde exactamente, entre 15 y 16, 466, se esconde √247, lo buscamos por la mitad de la calle, en el punto medio, es decir, sumamos 15 más 16,466 y lo dividimos entre 2: nos queda: 15,733.

¿Será 15,733 la raíz de 247? Dividimos 247 ente 15,733 y nos queda 15,699. Entre esos 2 números, entre 15,733 y 15,699 está escondido el que buscamos, √247. Vamos a buscarlo por el centro de la calle:

(15,733 + 15,699) / 2= 15,716

¿Será 15,716 el número buscado? Sí, si nos conformamos con tres decimales. Dividan 247 entre 15,716.

Alucinante, ¿no? Y más intuitivo, ¿no les parece? Solo hay que encontrar un número más pequeño, por ejemplo, que el que buscamos, un número que al cuadrado sea menor que el número del que nos han pedido la raíz, 247 en nuestro caso. Y a partir de ahí, solo hay que dividir y calcular una media. Lo resumimos en la siguiente tabla:

Es este un método más intuitivo, más fácil y que aproxima mejor la raíz cuadrada que el método clásico que nos enseñaron y nos siguen enseñando. Es el que yo enseñaría en primaria o secundaria... si tengo que enseñar a calcularla a mano, claro. Si me dejan, dedicaría este tiempo a enseñarles a pensar y a resolver problemas, y si nos sale una raíz cuadrada, la hacemos como una máquina. Por la misma razón que los alumnos no han llegado a clase en carretas tiradas por caballos.