Películas donde las matemáticas son las protagonistas

Son muchas las películas basadas en las matemáticas o, al menos, que tienen alguna relación con ellas. Aquí, por ejemplo, se puede encontrar un listado no completo. Sin embargo, la producción española o en español no es tan grande.

En muchas películas se llegan a mencionar las matemáticas, o alguna de sus ramas, pero en muy pocas ocupan un papel principal. Por eso destacamos tres de ellas en las que las matemáticas son absolutas protagonistas.

Evitaré, eso sí, 'Ágora' y otras películas conocidas y que le pueden venir a la mente al lector, porque en ellas las matemáticas -aunque aparecen- son muy secundarias en la trama.

Por orden cronológico, la primera y más desconocida para el público español es 'Moebius', dirigida en 1996 por el argentino Gustavo Daniel Mosquera.

Es esta una película extraña desde su concepción: el citado Gustavo Daniel Mosquera era profesor en la Universidad del Cine de Buenos Aires y llegó a sus manos un relato del prestigioso astrónomo norteamericano A.J. Deutsch llamado 'A subway named Moebius'.

En dicho relato, que transcurre en el metro de Boston, un convoy de metro desaparece... y no vamos a desvelar la trama, pero digamos que la banda de Moebius juega un papel protagonista y que para resolver el enigma se hará uso de ciertos conocimientos topológicos.

 

Mosquera vio en el relato una metáfora de los desaparecidos en la dictadura militar y así planteó un guión en el que acabaron colaborando seis alumnos suyos de la Universidad del Cine.

Después de más de un año, y tras muchas reescrituras, presentó el guión final a la dirección de su universidad y se aprobó un pequeño presupuesto para la realización de la película, contando con el apoyo y el trabajo de una compañera, María Ángeles Mira, y de 45 alumnos de la universidad.

La cuestión es que la película acabó teniendo bastante éxito tanto dentro como fuera de Argentina. Lo único malo es que, en todo el proceso, las matemáticas del relato original fueron perdiendo algo de sentido y se observa que entre los autores no había ningún especialista en la materia.

Una última curiosidad: como hemos dicho la película trata sobre la desaparición de un convoy de metro, en este caso en Buenos Aires... donde el teléfono de emergencia es también muy 'matemático': *31416.

La siguiente en el tiempo es 'La habitación de Fermat' de los españoles Luis Piedrahita y Rodrigo Sopeña.

Ya desde la primera frase se deja bien claro el protagonismo de las matemáticas en toda la trama: "¿Sabéis lo que son los números primos? Si no lo sabéis, mejor que os vayáis de aquí". Efectivamente, toda la trama gira alrededor de la conjetura de Goldbach, que afirma que todo número par mayor que 2 puede escribirse como la suma de dos primos.

De esta conjetura afirmó el prestigioso matemático británico Hardy en 1921 que posiblemente se trataba de uno de los problemas abiertos más difíciles de toda la matemática. Es de destacar que una versión más débil (en el sentido de que la fuerte implica la débil) de esta conjetura, que afirma que todo impar mayor que 5 se puede poner como la suma de tres primos, ha sido demostrada hace un par de años por Harald Helfgott.

Volviendo a la película en cuestión: cuatro matemáticos son invitados a una reunión si resuelven un enigma: "¿Qué patrón sigue la siguiente secuencia de números   5 – 4 – 2 – 9 – 8 – 6 – 7 – 3 – 1?"

No voy a resolver dicho enigma, lo dejo para el lector, pero sí comentar que desde el punto de vista matemático este tipo de cuestiones son un poco tramposas, ya que existe un resultado que nos dice que para cualquier serie finita de números podemos poner una regla matemática (los primeros valores de un polinomio) que la sigue, lo cual quiere decir que a cualquier serie finita de números puede seguir cualquier otro número.

El resto de la trama transcurre en una habitación cerrada y los cuatro matemáticos han de resolver diversos problemas si quieren salir con vida. Los problemas que se plantean están bien, pero tienen un inconveniente: todos, salvo uno, son muy, muy conocidos por los matemáticos, así que sería difícil que les plantearan ninguna dificultad.

El único que es menos conocido es el que requiere tratar de resolver qué se esconde tras esta serie de numeros:

000000000000000011111110000111111111110010001110001001001111100100111101011110011100100111000111111111000001000001000000100000100000011111110000000111110000000000 0000000

Pronto ven que hay 169 dígitos que forman la siguiente matriz 13x13:

0000000000000

0001111111000

0111111111110

0100011100010

0100111110010

0111101011110

0111001001110

0011111111100

0001000001000

0001000001000

0001111111000

0000111110000

0000000000000

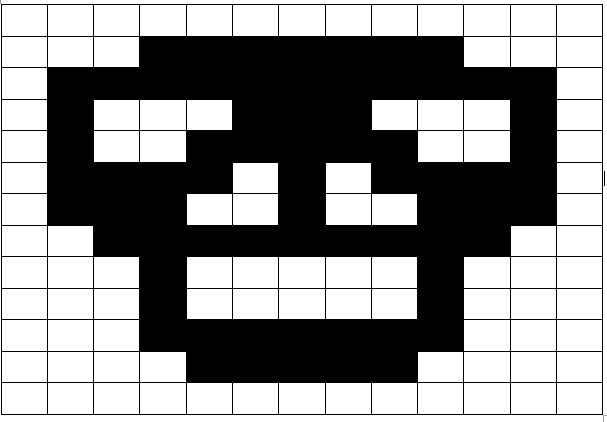
¿Ves ya de qué se trata? Si no es así, he dibujado esa matriz en una tabla 13x13 en la que las celdas que representan al 0 las he dejado en blanco y las que representan al 1 las he puesto de negro:

El resto de los enigmas, los que decía digo que son muy conocidos para todos los matemáticos, son

1.- Tenemos tres cajas de caramelos: una son de naranja, otra de limón, y la tercera los contiene mezclados. Las cajas vienen etiquetadas como "Naranja", "Limón" y "Mezcla", pero se sabe que las tres etiquetas son incorrectas.

¿Cuántos caramelos será necesario probar para conocer el contenido de cada caja?

2.- En el sótano hay tres llaves de luz y en el tercer piso están las bombillas que se encienden con cada una de esas llaves. No se sabe qué llave corresponde a cada foco y la única manera de averiguarlo sería usando la llave y subir al tercer piso para comprobar. ¿Cuál es el procedimiento para subir la menor cantidad de veces al tercer piso y conocer qué llave le corresponde a cada bombilla?

3.- Dos puertas, dos guardianes (uno que siempre miente, y otro que siempre dice la verdad), una puerta lleva a la salida del laberinto y la otra solo te mantiene en el laberinto. Solo se puede hacer una pregunta a un solo guardián. Las dos puertas se perciben iguales, los dos guardianes también. ¿Qué pregunta hacer para escoger la puerta correcta?

4.­ Un colega le pregunta al profesor Otto las edades de sus tres hijas y este responde que el producto de sus edades es igual a 36 y que la suma es igual al número del portal de enfrente. El colega mira el portal en cuestión y, tras pensar un momento, dice: "La mayor toca el piano". ¿Qué edades tienen las tres hijas del Profesor Otto?

5.-  ¿Cómo medir 9 minutos con dos relojes de arena de 4 y 7 minutos?

Si no han visto la película pueden entretenerse con los anteriores acertijos un buen rato.

Hemos hablado hasta ahora de una película argentina y de otra española, ahora toca el turno a la última en la que tenemos participación de ambos países (realmente en 'La habitación de Fermat' también hay alguna participación argentina, ya que uno de los protagonistas es Federico Luppi). Se trata de 'Los crímenes de Oxford', del español Alex de la Iglesia y con un guión basado en el libro del mismo título (al menos en España) del escritor y matemático argentino Guillermo Martínez.

En ella se suceden una serie de crímenes y se trata de averiguar la secuencia lógica llevada a cabo por el asesino, en medio de numerosas discusiones sobre matemáticas y filosofía.

Es curioso como algunos críticos la tachan de incomprensible solo por falta de cultura, ya que la ciencia es cultura y desconocerlo no es más que ignorancia. Otros echan en falta que se parezca más a 'Pi, fe en el caos', que sí es mucho más hermética y que contiene errores matemáticos de bulto. No es que sea mi película favorita, honestamente, pero me alegra que la fascinación por las matemáticas de algunos autores encuentren su hueco en el cine.

Ya ven, las matemáticas no solo son útiles y bellas sino que además dan para guiones de cine muy enrevesados y entretenidos