¿Qué pueden hacer las matemáticas por tus selfies?

Estamos en verano y es, posiblemente, la época del año en la que más fotografías hacemos. Aprovechamos que estamos de vacaciones para 'castigar' a nuestros seres queridos enviándoles imágenes de esos sitios maravillosos en los que estamos y a los que ellos no han podido venir (o de nuestros pies en la arena, vaya).

Para ello, casi todos hacemos uso de nuestros móviles o cámaras digitales. Existen también otros métodos para enviar imágenes que no usan esos dispositivos sino otros más primitivos que se llaman postales, ¿se acuerdan?

Pues bien, si se fijan, casi todas las imágenes que sacamos están almacenadas en unos archivos que tienen la extensión .jpg pero ¿qué es un archivo JPG? De eso venimos a hablar hoy y de, cómo no, el papel fundamental de las matemáticas en la creación de los mismos.

El nombre JPG proviene de JPEG que son las siglas de Joint Photographic Experts Group, grupo que en los años noventa del pasado siglo fijaron una serie de normas (o pasos) para comprimir una imagen, esto es: tratar de almacenar la información más significativa de una imagen usando un almacenamiento relativamente reducido.

Con ello se ha permitido que se puedan enviar imágenes (que pesan poco) por internet y que las podamos almacenar sin necesidad de gastar todo nuestros ahorros en discos duros. Como no podía ser de otra forma y ya hemos avisado, para obtener un archivo JPG se usan muchas matemáticas. Vamos a tratar de comentar aquí de forma general cuáles son dichas herramientas: nos esperan matrices, cosenos, divisiones y redondeos, que nadie se asuste

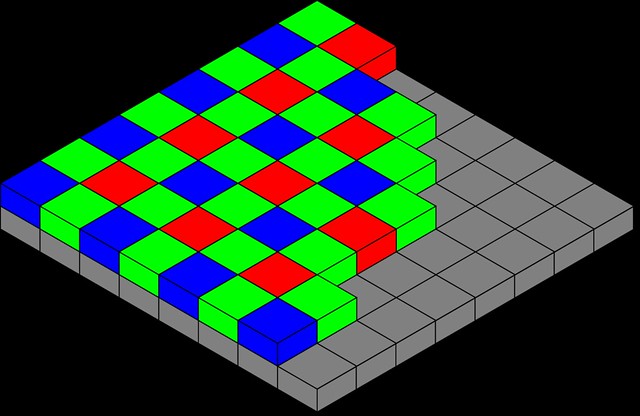
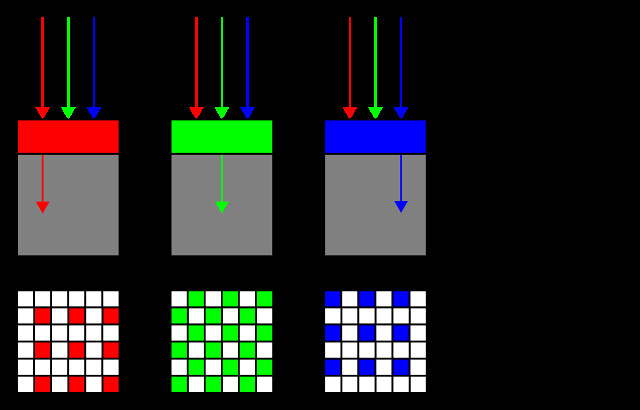
Lo primero que tenemos que entender es cómo captura la imagen nuestra cámara fotográfica. La parte fundamental es el sensor: lLos hay de distintos tipos pero básicamente son una cuadrícula de pequeños sensores (llamados fotositos) que captan la intensidad de luz que incide en ellos. Ojo, el sensor de nuestra cámara no capta el color, solo la intensidad de luz, lo que ocurre es que a algunos fotositos les ponemos un filtro verde, a otros un filtro rojo y a otros un filtro azul.

Por lo tanto, a cada fotosito solo le llega la luz de uno de los tres colores básicos. Estos fotositos están agrupados siguiendo un esquema específico para cada cámara, la mayoría de las cámaras usan la disposición del patrón de Bayer que es muy simple:

Podemos ver que hay el doble de fotositos verdes que de los otros colores. Esto es debido a que la sensibilidad del ojo humano capta mejor las variaciones de luminosidad para el verde (al parecer, por una cuestión evolutiva). Así, cada pixel de nuestro selfie estará definido por 4 fotositos de este patrón.

Pues bien, cada fotosito da un valor de la intensidad de su color expresado como un número entre 0 (el fotosito no ha captado nada de ese color) y 255 (estamos captando el máximo de luz de ese color). Una imagen, por lo tanto, la podemos considerar como tres tablas (una para cada color) que solemos llamar 'matrices', donde cada entrada de la tabla o matriz es un número entre 0 y 255.

Si almacenamos esas tres matrices tendremos la imagen tal y como la ha captado nuestra cámara, pero eso nos daría lugar a ficheros enormes por cada imagen y no ganaríamos para memoria. Los ficheros RAW, que usan casi todos los profesionales y aficionados avanzados, sí que guardan (de forma más o menos eficiente) todos los números de esas tres matrices.

Mucho estoy hablando ya de matrices, ¿no? Por si alguien no lo recuerda o no lo sabe, una matriz es simplemente una tabla con números. Un cachito de una matriz obtenida de una fotografía es algo así como esto:

5	176	193	168	168	170	167	165
6	176	158	172	162	177	168	151
5	167	172	232	158	61	145	214
33	179	169	174	5	5	135	178
8	104	180	178	172	197	188	169
63	5	102	101	160	142	133	139
51	47	63	5	180	191	165	5
49	53	43	5	184	170	168	74

Sí, es verdad, es Más bonita que muchas de las fotos que nos mandan por Whatsapp. Sigo, que me derivo.

La clave de JPEG está en almacenar (casi) toda la información de dicha matriz, pero ocupando muchísimo menos espacio. Para ello es importante saber que si una matriz tiene muchos ceros, es menos costoso almacenarla. Y si además dichos ceros están todos juntitos mejor que mejor. ¿Por qué? Pues porque si tenemos que escribir 16 ceros seguidos podremos acortarlo con 16(0): es la misma información pero en 5 caracteres en lugar de 16 -si son usuarios de Twitter también le verán la ventaja-.

Bueno, ¿y cómo conseguimos que haya muchos ceros en nuestras matrices, que estén muy juntitos, que no se pierda calidad de la foto y que sea un proceso (casi) reversible?

Ajá, con muchas matemáticas.

El primer paso consiste en pasar de las tres matrices iniciales (las del rojo, verde y azul) y quedarse con otras tres matrices que describirán la luminosidad, la proporción entre azul y rojo y la proporción entre verde y rojo. Ello se consigue con una simples ecuaciones. Por ejemplo, el cambio de los tres colores a luminosidad viene dado por la ecuación:

Y= 0,257 * R + 0,504 * G + 0,098 * B + 16

(en la que R, G y B son los valores de un pixel dado en las matrices del rojo, del verde y del azul respectivamente).

Las otras dos ecuaciones son:

Cb = U = -0,148 * R - 0,291 * G + 0,439 * B + 128

Cr = V =  0,439 * R - 0,368 * G - 0,071 * B + 128

Para el que sepa de operaciones entre matrices, todo esto se puede hacer con multiplicaciones y sumas de matrices, y se puede comprobar que es una operación reversible (y sencillita)

Sigo. Son estas tres nuevas matrices las que vamos a transformar con pasos fijos para conseguir que tengan muchos ceros y que estén todos seguidos.

Primero dividimos cada matriz en submatrices de 8x8 (estos son los 8 bits del JPG) como la que pusimos al principio del artículo. Después, a cada número le restamos 127 (los valores pueden variar para las distintas matrices de luminosidad o color) para que los valores estén centrados alrededor del 0. Con esto la matriz de nuestro ejemplo quedaría así:

-122	49	66	41	41	43	40	38
-121	49	31	45	35	50	41	24
-122	40	45	105	31	-66	18	87
-94	52	42	47	-122	-122	8	51
-119	-23	53	51	45	70	61	42
-64	-122	-25	-26	33	15	6	12
-76	-80	-64	-122	53	64	38	-122
-78	-74	-84	-122	57	43	41	-53

El siguiente paso puede parecer más complejo pero se trata simplemente de aplicar una fórmula a los números de cada submatriz 8x8. Esa fórmula se llama 'transformada discreta del coseno' y es (la podéis encontrar aquí) muy similar a la transformada de Fourier que se utiliza en numerosos campos como el procesamiento de la imagen o del sonido.

El resultado de aplicar la transformada discreta del coseno a nuestra matriz es:

-27.500	-213.468	-149.608	-95.281	-103.750	-46.946	-58.717	27.226
168.229	51.611	-21.544	-239.520	-8.238	-24.495	-52.657	-96.621
-27.198	-31.236	-32.278	173.389	-51.141	-56.942	4.002	49.143
30.184	-43.070	-50.473	67.134	-14.115	11.139	71.010	18.039
19.500	8.460	33.589	-53.113	-36.750	2.918	-5.795	-18.387
-70.593	66.878	47.441	-32.614	-8.195	18.132	-22.994	6.631
12.078	-19.127	6.252	-55.157	85.586	-0.603	8.028	11.212
71.152	-38.373	-75.924	29.294	-16.451	-23.436	-4.213	15.624

Estos valores tienen la propiedad que los más significativos están en la parte izquierda-arriba de la matriz.

Ya solo nos queda un paso (más la codificación). Es importante señalar que todo lo que hemos hecho hasta ahora es reversible y que, por lo tanto, no implica una compresión ni pérdida de calidad. El siguiente paso, sin embargo, sí conlleva una pérdida de calidad: dividimos cada elemento de la matriz resultante por un número (estos números serán mayores si pedimos mayor nivel de compresión y menores si exigimos más calidad).

Por ejemplo, los valores usados para una compresión del 50% son los siguientes:

Así dividimos -27.500 entre 16 y lo aproximamos al entero más cercano (-2), dividimos -213.468 entre 11 para obtener -19 y así sucesivamente hasta obtener los siguientes valores:

-2	-19	-15	-6	-4	-1	-1	0
14	4	-2	-13	0	0	-1	-2
-2	-2	-2	7	-1	-1	0	1
2	-3	-2	2	0	0	1	0
1	0	1	-1	-1	0	0	0
-3	2	1	-1	0	0	0	0
0	0	0	-1	1	0	0	0
1	0	-1	0	0	0	0	0

Como hemos dividido por número relativamente grandes (sobre todo en la parte abajo-derecha), muchos de los valores son 0, que es justamente lo que queríamos. Y esta es la matriz que almacenamos (recorriéndola en zigzag).

Naturalmente a partir de esta última matriz podemos recuperar todos los pasos anteriores, aunque, como hemos hecho un redondeo al dividir, no obtendremos exactamente la imagen original sino una que se le parece muchísimo.

Alucinante, ¿verdad? Pueden llorar de emoción. Yo lo hice cuando me lo contaron.

Existen otro métodos para comprimir imágenes, pero este es el más utilizado, aunque no sea el más eficiente. Por ejemplo, el grupo de JPEG ya ha sacado un nuevo método, llamado JPEG-2000 que utiliza otras herramientas más sofisticadas que la transformada discreta del coseno. Pero esto se los cuento otro día porque tiene asociada la historia de un futbolista muy famoso.

Ea, pueden seguir con sus fotos de vacaciones.