Una tablilla babilónica muestra el ejemplo de geometría aplicada más antiguo del mundo

En 2017 el profesor Daniel Mansfield de la Universidad de Nueva Gales del Sur (UNSW, Australia) descubrió que una tablilla rectangular babilónica denominada Plimpton 322, de unos 3.800 años de antigüedad, era la tabla trigonométrica más antigua y precisa del mundo.

Ahora, Mansfield ha publicado en la revista Foundations of Science un nuevo estudio con más detalles sobre esa pieza de arcilla y sobre otra redonda —una tablilla de mano para llevar cómodamente en la mano— que llevaba más de un siglo olvidada en el Museo Arqueológico de Estambul (Turquía).

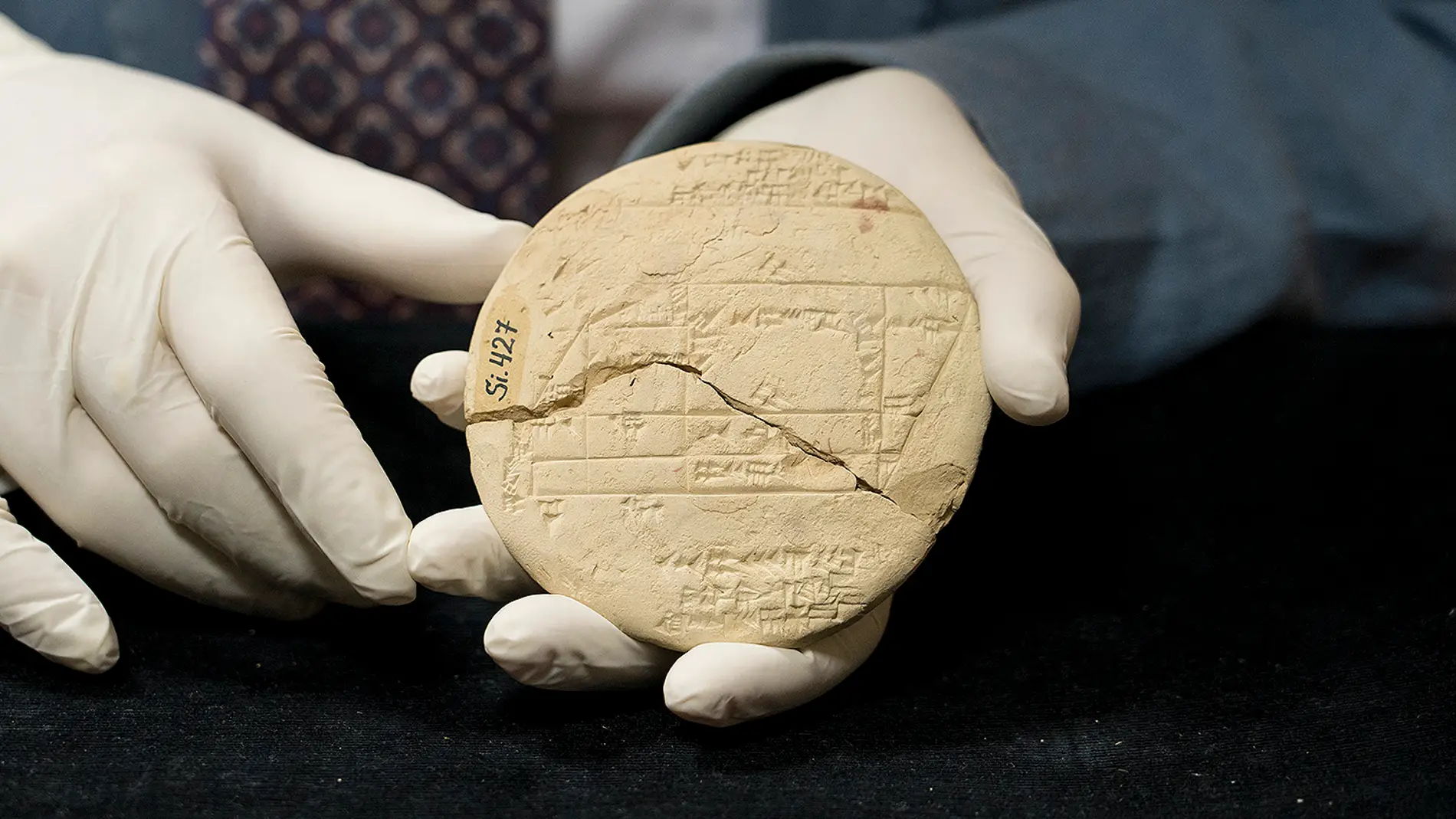
La tablilla, etiquetada como Si.427 y fechada en la Antigua Babilonia entre el 1900 y 1600 a.C., es el único ejemplo conocido de un documento catastral de esa época, un plano utilizado por los topógrafos para definir los límites de las tierras

Está etiquetada como Si.427 y fue recogida en 1894 por el arqueólogo francés Vincent Scheil en Sippar, una ciudad de la Baja Mesopotamia situada en lo que hoy es la provincia de Bagdad, en Irak. Según Mansfield, es el ejemplo más antiguo de geometría aplicada del que se tiene constancia.

“Si.427 data del período de la Antigua Babilonia (entre el 1900 y 1600 a.C.)”, afirma este matemático, y según confirma a SINC, “lo sabemos porque la tablilla hace referencia a un campo propiedad de Sîn-bêl-apli, un terrateniente que vivía en Sippar en esa época, y además el estilo del lenguaje lo confirma”.

“Es el único ejemplo conocido de un documento catastral de ese periodo –subraya–, un plano utilizado por los topógrafos para definir los límites de las tierras. En este caso, nos informa de los detalles legales y geométricos de unas tierras (pantanosas o humedales) divididas tras la venta de una parte”.

Ternas pitagóricas antes de Pitágoras

Pero si hay algo que destaca en esta milenaria arcilla es el uso de lo que hoy se conoce como ternas pitagóricas para hacer ángulos rectos precisos. Mansfield destaca que este descubrimiento tiene importantes implicaciones para la historia de las matemáticas, ya que aparece esta figura geométrica mil años antes de que naciera Pitágoras.

Este descubrimiento tiene importantes implicaciones para la historia de las matemáticas, ya que aparecen ternas pitagóricas mil años antes de que naciera Pitágoras

“Una terna pitagórica es un triángulo rectángulo (o rectángulo) de medidas muy simples que satisface el teorema de Pitágoras —explica—. La mayoría de los rectángulos y triángulos rectos tienen longitudes muy incómodas como 1,4142135623730951..., pero estas ternas tienen medidas muy sencillas como 3,4 y 5. Esto hace que sean una forma fácil de construir líneas perpendiculares, y se utilizó en la antigua India ya en el año 800 a.C., pero ahora sabemos que también en la topografía babilónica en el año 1900 a. C., unos mil años antes”.

En el caso de la tablilla redonda, escrita con letra cuneiforme, se dibuja el campo vendido con líneas de cuadrícula horizontales y verticales superpuestas, lo que permitió al topógrafo realizar una precisa subdivisión. En concreto, la tablilla contiene las ternas 5-12-13 (dos veces) y la 8-15-17, que se emplearon como guía teórica para las líneas perpendiculares de la cuadrícula.

Otras tablillas de la época también mencionan disputas de Sîn-bêl-apli por temas relacionados con sus tierras, como en una donde se menciona un pleito con otra rica terrateniente por las valiosas palmeras datileras que crecían entre sus dos propiedades. Un administrador local aceptó enviar a un topógrafo para resolver el conflicto, un ejemplo más de lo importante que era ya entonces establecer las límites catastrales.

“Sabíamos que los babilonios conocían los triángulos rectángulos y las ternas o ‘triples’ pitagóricos, pero desconocíamos por y para qué”, apunta el investigador, “pero ahora la nueva tablilla Si.427 nos muestra que usaban estas formas para medir con precisión el terreno, y esto nos ayuda a entender otras tablillas de la misma época, como la más famosa Plimpton 322”. En 2017 ya se planteó que esta tuviera algún propósito práctico para construir palacios, templos, canales... o en la topografía de campos.

Mansfield considera que la forma en que se establecen los límites entre las tierras revela una verdadera comprensión geométrica: “Nadie esperaba que los babilonios utilizaran las ternas pitagóricas de esta manera. Se trata de algo más parecido a las matemáticas puras, inspirado en los problemas prácticos de la época”.

En general, se acepta que la trigonometría (la rama de las matemáticas que se ocupa del estudio de los triángulos) fue desarrollada por los antiguos griegos al estudiar el cielo nocturno en el siglo II antes de Cristo, pero estudios como este demuestran que los babilonios desarrollaron su propia 'proto-trigonometría' alternativa para resolver problemas relacionados con la medición del suelo, no del cielo.

Crear ángulos rectos: más fácil de decir que de hacer

Una forma sencilla de crear un ángulo recto exacto es hacer un rectángulo con los lados 3 y 4, y la diagonal 5. Estos números especiales forman la terna pitagórica 3-4-5, y un rectángulo con estas medidas tiene ángulos rectos matemáticamente perfectos. Era importante para los topógrafos de la antigüedad y todavía se utiliza hoy en día.

“Los antiguos topógrafos que grabaron el Si.427 hicieron algo aún mejor: utilizaron una variedad de diferentes ternas pitagóricas, tanto en forma de rectángulos como de triángulos rectos, para construir ángulos rectos precisos”, señala el matemático australiano.

Sin embargo, es difícil trabajar con números primos mayores de 5 en el sistema numérico babilónico que era de base 60. “Esto plantea un problema muy particular: su sistema numérico único de base 60 significa que solo se pueden utilizar algunas formas pitagóricas”, explica Mansfield, “y parece que el autor de Plimpton 322 recorrió todas esas formas para encontrar aquellas útiles”.

El misterio del 25:29

Solo queda un misterio que el autor no ha conseguido todavía desvelar: en el reverso de la tablilla, en la parte inferior, aparece el número sexagesimal “25:29” en letra grande, y el matemático piensa que son 25 minutos y 29 segundos.

“No puedo entender qué significan estos números, es un absoluto enigma —reconoce—. Estoy deseando debatir cualquier pista con historiadores o matemáticos que puedan tener una corazonada sobre lo que estos números tratan de decirnos”, concluye.

Referencia:

Daniel F. Mansfield. “Plimpton 322: A Study of Rectangles”. Foundations of Science, 2021